|
Contar Mal |
| ¿Alguien se ha dado cuenta de que no estoy haciendo tablas ni nada sobre esta temporada de PTQs? ¿No? Os odio. |
La segunda parte de este artículo apareció dos semanas después, está aquí.
Sí que estoy haciendo algo, lo que no sé es qué. En realidad llevo desde que empezó el año cocinando, pero me cogió el toro, porque pensaba que los PTQs empezaban en Marzo. En Marzo empiezan en Andalucía, pero como todo el mundo sabe, España se acaba en Despeñaperros.
Hay varios problemas con lo que he estado haciendo y cómo lo he estado haciendo -me refiero a esto, si alguien es nuevo- y ya hacía falta un lavado de cara. Lo principal son los métodos para recoger barajas y procesarlas (mis scripts.) La mayoría del proceso ya estaba semi automatizado, pero me quedaban dos cuellos de botella importantes: comprobar las barajas y clasificarlas en arquetipos.
Para asegurarme de que las barajas tenían cartas correctas, las importaba en el Magic WorkStation una a una, y aprovechaba para mirarlas y asignarles un arquetipo. Para eliminarme a mí del proceso y de paso el MWS, necesitaba algo más potente que el pseudolenguaje que estaba utilizando, así que me pasé a python. Lo estoy portando y unificando todo, así será más versátil y rápido, que era el objetivo.
Una de las cosas que voy a hacer de ahora en adelante, cada temporada, es poner cierta información sobre cada arquetipo, en hilos cerrados, como referencia. Información que actualizaré periódicamente. No tengo claro que información hasta que termine todas mis herramientas, pero algo que ya tenía y nunca publiqué es el porcentaje de uso de cada carta -como ya muestra mtgstats, ¡te me has adelantado, maldito!-, la intersección de todas las listas -que yo llamo esqueleto del arquetipo- y otras medidas estadísticas centrales (la moda de cada carta es lo más útil).
En realidad, así es como yo hago listas "stock" de un arquetipo: miro cada carta que esté en el 60% o más de las listas y me quedo con la moda (la moda es el valor más común de una distribución, no unos pantalones de medio sueldo), hasta que tenga las 75. La moda tiene una ventaja, que es un valor que siempre tiene sentido en la distribución, no es fraccionario como es típicamente la media.
Para poder comprobar y corregir las listas con un script en python, sin pasar por el MWS, necesitaba poder acceder a la información sobre como mínimo nombres de cartas y formato en el que son legales. Aprovechando la coyuntura, incorporé el resto de información (color, etc.) y se me ocurrió taggear (etiquetar) cada carta con alguna reducción subjetiva que pudiera ser útil. De momento sólo he taggeado las cartas del Extendido actual, y muy pocas cartas manualmente, así que habrá fallos, pero es un comienzo. Si no sabeis lo que quiero decir, mirad el árbol de tags:
Cuando un tag es hijo de otro, significa que sus padres se querían mucho, pero luego se divorciaron y ahora se tratan como los trapos. Que típico. Un tag hijo nunca aparece sin el padre: si una carta tiene el tag 'aura', entonces en todos los casos también tiene 'enchantment' y 'permanent'.
Las primeras familias y 'tribal' no tienen mucha chicha, es su línea de tipos y punto. Pero sólo con eso ya puedo distinguir entre tierras ('lands') y no tierras (cualquier otro), y por ejemplo ahora sé automáticamente que la moda de las tierras de Faeries es 26. Al menos hasta mitad de Enero, que fué la última vez que actualicé esos datos.
A partir de ahí ya se pone más interesante. ¿'Disruption' y 'removal' en Faeries? Modas 28 y 17 -dos de ellos 'mass', masivo- en las 75. 26 y 10 maindeck, respectivamente.
Lamentablemente, los tags más útiles son también los más subjetivos... El 'bouncing' lo he considerado 'removal' por su uso competitivo, en el sentido de que subir según qué permanente a la mano en el turno decisivo podría darte la victoria (un Prismatic Omen, un bloqueador o yo que sé). También se podría considerar 'disruption', subiendo generadores de maná, pero WoTC ya no gusta de forzar esos efectos para competición (ni Boomerang es legal en Extendido), así que me pareció menos relevante. Vendilion Clique no es exactamente descarte, pero es el tag que le he puesto. Habrá muchos más ejemplos, y estoy abierto a sugerencias.
Me faltan tags como 'card advantage' o 'card selection', pero esos eran difíciles de asignar sin tener que hacerlo demasiado a mano y lo dejé. Es un comienzo, ya digo.
Clasificar arquetipos programáticamente no iba a ser tan sencillo. Es lo que me está llevando mes y pico, con pausa para hacerme el Dead Space 2, por supuesto.
Supongo que debería empezar por el principio. La primera pregunta que se tiene uno que hacer es ¿qué es un arquetipo? Puedo concebir dos definiciones, una cualitativa y otra cuantitativa:
- Dos barajas pertenecen al mismo arquetipo si tienen ciertas cartas similares o iguales, de forma que "juegan de la misma manera" (cualitativa).
- Dos barajas pertenecen al mismo arquetipo si tienen suficientes cartas iguales (cuantitativa).
Con la definición cuantitativa ya sí estamos hablando en serio. ¿Número de cartas iguales? ¡Fuck yeah, eso se puede medir! ¡Muerte al Papa!
Pero ni siquiera esa es completamente precisa. ¿"Suficientes cartas iguales"? ¿Cuanto es "suficiente"? Pues suficiente es suficiente, obviamente.
Lo primero es no tener en cuenta los banquillos en las comparaciones, porque varían demasiado. Un valor intuitivo para el umbral para pertenecer al msimo arquetipo puede ser el 50%. Si no tienen al menos la mitad del maindeck iguales, no tienen pinta de estar en el mismo arquetipo. Me puse a explorar que tipo de valores se daban y llegué a un algoritmo intuitivo pero primitivo.
El objetivo es clasificar un conjunto arbitrariamente grande de barajas en subconjuntos que pueda llamar arquetipos, para luego etiquetarlos yo (eso es imposible de automatizar). En realidad, esto es buscar una partición del conjunto (conjunto de subconjuntos disjuntos cuya unión es el conjunto original). El número de particiones posibles de un conjunto es muy grande, crece exponencialmente con el tamaño del conjunto. La partición óptima no se puede calcular en tiempo razonable, sólo podemos buscar un óptimo local (optimal).
- Para cada baraja, calculaba el conjunto de barajas cuyo porcentaje de similitud con ella superaba el umbral, incluyendo ella misma (100% de similitud consigo misma, supera cualquier umbral.) Gráficamente, esto es como dibujar una nube de puntos, representando cada baraja, y dibujo un círculo agrupando cada baraja que sea lo suficientemente similar. En este punto, cualquier conjunto con un sólo elemento, es un rogue deck y forma parte de su propio arquetipo. Los considero solucionados y los largo.
- Ahora, para cada conjunto único (considero cada conjunto distinto sólo una vez), calculo el conjunto de los conjuntos que tienen alguna intersección con el, incluyendo el mismo. Es decir, pongo juntos los conjuntos de barajas similares que compartan alguna baraja. Gráficamente, estoy mirando todos los circulitos que he dibujado antes y viendo cuáles están solapados. En este punto, cualquier círculo que no solape con ningún otro es un arquetipo. Los considero solucionados y los largo.
- Con los conjuntos únicos que me quedan del paso anterior, vuelvo a calcular conjuntos de conjuntos con intersección no vacía. Esto es como alejarme más y delimitar "regiones independientes." De nuevo, cualquier conjunto independiente debe de ser un arquetipo.
- ...
- Profit.
Esto era un método muy burdo, y no podía aplicarlo a más de unas 80-100 barajas por vez, o corría el riesgo de que hubieran demasiadas barajas de estas que encajan mal y deforman los arquetipos. Apenas ganaba tiempo respecto a clasificarlas a mano, pero encima perdía muchísima precisión (nada más preciso que uno mismo.) En este callejón sin salida me quedé. Me puse con otras cosas, pensando que quedaba mucho para la siguiente temporada de PTQs. Era como Septiembre, después de todo.
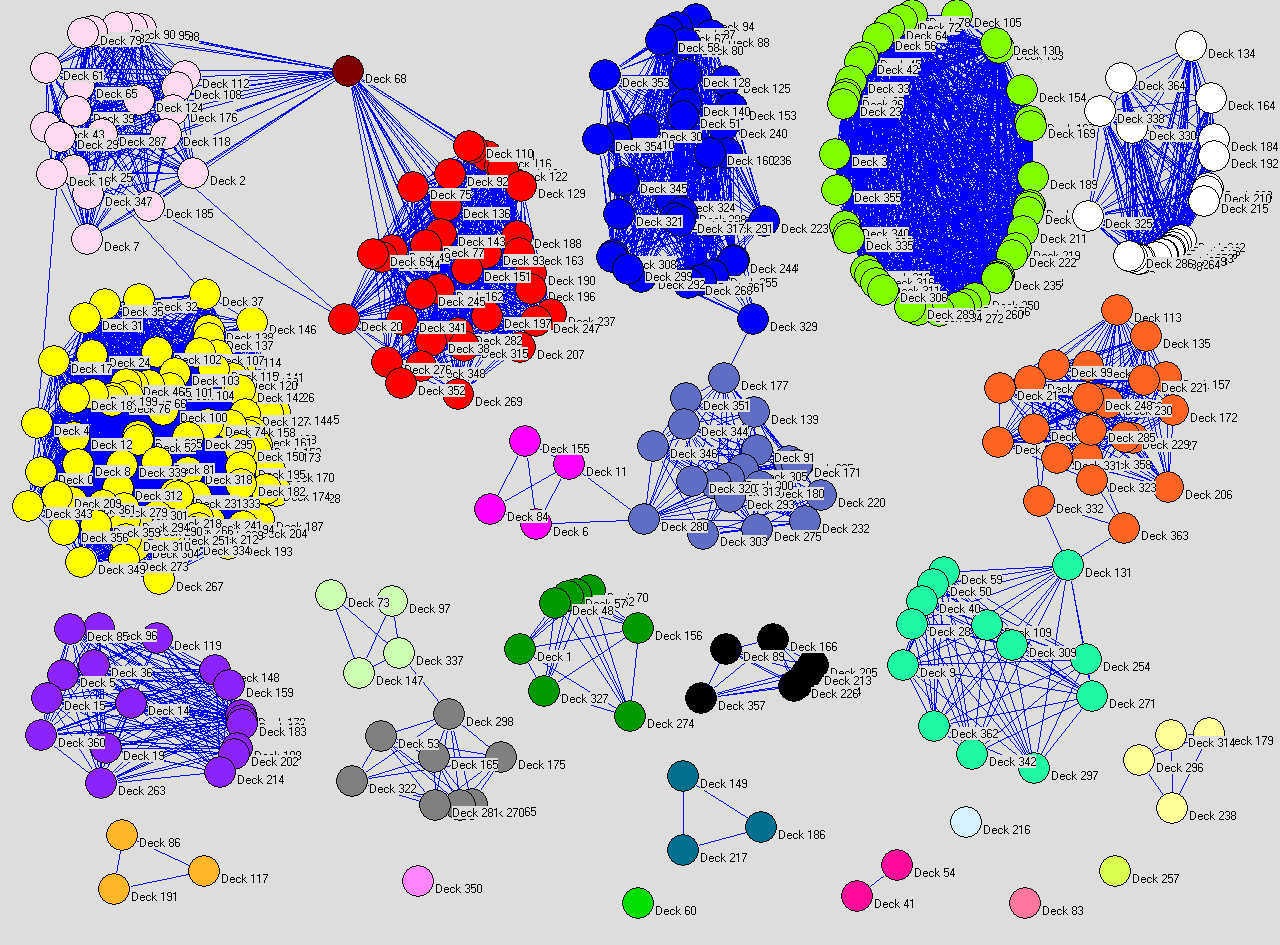
Los primeros días de Enero, me estaba documentando sobre otra cosa y por casualidad me topé con algo sospechosamente parecido a mi problema. Resulta que si represento las relaciones de similitud como un grafo, con las barajas como nodos, el problema se llama "Búsqueda de Comunidades en Redes Complejas."
Una red compleja no es más que un grafo denso, y una comunidad es un subconjunto de nodos que cumpla algo. El origen de este problema es encontrar la organización que pueda haber en redes sociales, por eso el nombre de "comunidad." Clasificar barajas en arquetipos resulta ser un caso concreto relativamente simple. A pesar de que representa un grafo cerca de estar completo (en un grafo completo todos los nodos tienen relacion con todos los demás, no puede ser más denso), son poco más que miles de nodos, mientras que los grafos que intenta solucionar este problema pueden tener millones de nodos. Además, sabemos que los arquetipos existen y, salvo algunos casos, deben de estar claramente separados, así que son más fáciles de detectar que en otro grafo que represente cosas menos estrictas y más arbitrarias, como las comunicaciones entre personas de una red de chat de móviles en Bélgica.
Apenas he empezado a hablar del verdadero avance, que era este, pero tendré que dejarlo para una segunda parte. Aunque para el viernes que viene espero haber puesto la manteca en el foro y publicar la primera tabla de la temporada. Al menos no me quiero ir sin poner esto:
BEHOLD!
¡Extendido! O al menos hasta mitad de Enero."La Leyenda de la Baraja 68" es un buen título para una novela.
No pienso soltar prenda sobre quién es quién. Bueno vale, el amarillo canario es Faeries y el círculo verde lima es Jund.
Hasta la próxima y recordad:
Everything that is simple, is theoretically false, everything that is complicated is pragmatically unusable.
Todo lo que es simple, es teóricamente falso, todo lo que es complicado es pragmáticamente inusable.
-Paul Valery